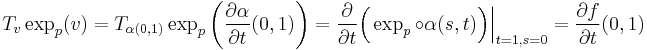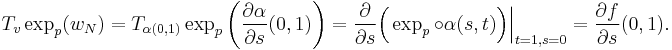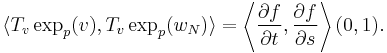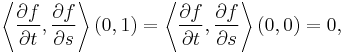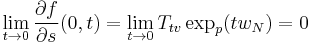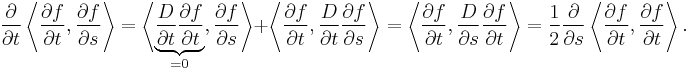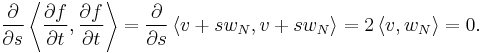Gauss's lemma (Riemannian geometry)
In Riemannian geometry, Gauss's lemma asserts that any sufficiently small sphere centered at a point in a Riemannian manifold is perpendicular to every geodesic through the point. More formally, let M be a Riemannian manifold, equipped with its Levi-Civita connection, and p a point of M. The exponential map is a mapping from the tangent space at p to M:
which is a diffeomorphism in a neighborhood of zero. Gauss' lemma asserts that the image of a sphere of sufficiently small radius in TpM under the exponential map is perpendicular to all geodesics originating at p. The lemma allows the exponential map to be understood as a radial isometry, and is of fundamental importance in the study of geodesic convexity and normal coordinates.
Contents |
Introduction
We define on  the exponential map at
the exponential map at 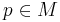 by
by
where we have had to restrict the domain 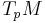 by definition of a ball
by definition of a ball 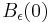 of radius
of radius 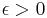 and centre
and centre 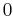 to ensure that
to ensure that 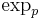 is well-defined, and where
is well-defined, and where 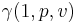 is the point
is the point 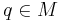 reached by following the unique geodesic
reached by following the unique geodesic 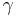 passing through the point
passing through the point 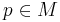 with tangent
with tangent 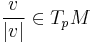 for a distance
for a distance 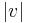 . It is easy to see that
. It is easy to see that 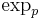 is a local diffeomorphism around
is a local diffeomorphism around 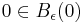 . Let
. Let 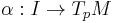 be a curve differentiable in
be a curve differentiable in 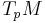 such that
such that 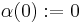 and
and 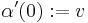 . Since
. Since 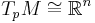 , it is clear that we can choose
, it is clear that we can choose 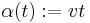 . In this case, by the definition of the differential of the exponential in
. In this case, by the definition of the differential of the exponential in 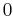 applied over
applied over 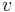 , we obtain:
, we obtain:
The fact that 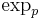 is a local diffeomorphism and that
is a local diffeomorphism and that 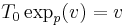 for all
for all 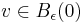 allows us to state that
allows us to state that 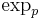 is a local isometry around
is a local isometry around 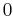 , i.e.
, i.e.
This means in particular that it is possible to identify the ball 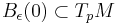 with a small neighbourhood around
with a small neighbourhood around 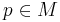 . We can see that
. We can see that 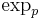 is a local isometry, but we would like it to be rather more than that. We assert that it is in fact possible to show that this map is a radial isometry !
is a local isometry, but we would like it to be rather more than that. We assert that it is in fact possible to show that this map is a radial isometry !
The exponential map is a radial isometry
Let 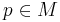 . In what follows, we make the identification
. In what follows, we make the identification 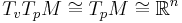 .
.
Gauss's Lemma states: Let 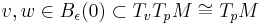 and
and 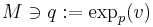 . Then,
. Then, 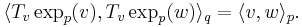
For 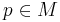 , this lemma means that
, this lemma means that 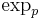 is a radial isometry in the following sense: let
is a radial isometry in the following sense: let 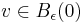 , i.e. such that
, i.e. such that 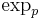 is well defined. And let
is well defined. And let 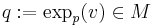 . Then the exponential
. Then the exponential 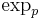 remains an isometry in
remains an isometry in 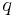 , and, more generally, all along the geodesic
, and, more generally, all along the geodesic 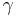 (in so far as
(in so far as 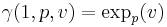 is well defined)! Then, radially, in all the directions permitted by the domain of definition of
is well defined)! Then, radially, in all the directions permitted by the domain of definition of 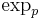 , it remains an isometry.
, it remains an isometry.
Proof
Recall that
We proceed in three steps:
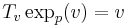 : let us construct a curve
: let us construct a curve
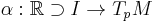 such that
such that 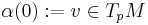 and
and 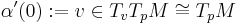 . Since
. Since 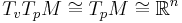 , we can put
, we can put 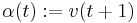 . We find that, thanks to the identification we have made, and since we are only taking equivalence classes of curves, it is possible to choose
. We find that, thanks to the identification we have made, and since we are only taking equivalence classes of curves, it is possible to choose 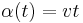 (these are exactly the same curves, but shifted because of the domain of definition
(these are exactly the same curves, but shifted because of the domain of definition  ; however, the identification allows us to gather them around
; however, the identification allows us to gather them around  . Hence,
. Hence,
Now let us calculate the scalar product 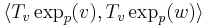 .
.
We separate 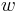 into a component
into a component 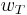 parallel to
parallel to 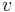 and a component
and a component 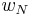 normal to
normal to 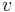 . In particular, we put
. In particular, we put 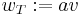 ,
, 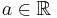 .
.
The preceding step implies directly:
We must therefore show that the second term is null, because, according to Gauss's Lemma, we must have:
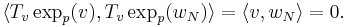
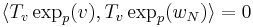 :
:
Let us define the curve
Note that
Let us put:
and we calculate:
and
Hence
We can now verify that this scalar product is actually independent of the variable 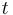 , and therefore that, for example:
, and therefore that, for example:
because, according to what has been given above:
being given that the differential is a linear map! This will therefore prove the lemma.
- We verify that
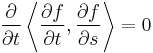 : this is a direct calculation. Since the maps
: this is a direct calculation. Since the maps 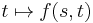 are geodesics,
are geodesics,
Since the maps 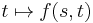 are geodesics, the function
are geodesics, the function 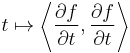 is constant. Thus,
is constant. Thus,
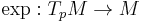
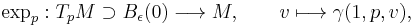
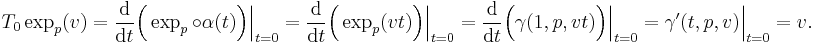
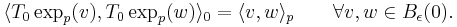
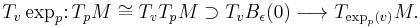
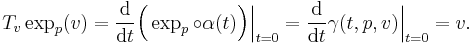
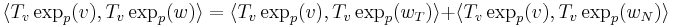
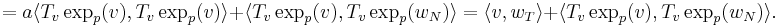
![\alpha \colon [-\epsilon, \epsilon]\times [0,1] \longrightarrow T_pM,\qquad (s,t) \longmapsto tv%2Btsw_N.](/2012-wikipedia_en_all_nopic_01_2012/I/b8c0f4c7b12a2e731381f5e5e0e9c84e.png)
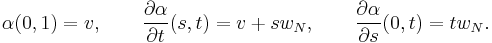
![f \colon [-\epsilon, \epsilon ]\times [0,1] \longrightarrow M,\qquad (s,t)\longmapsto \exp_p(tv%2Btsw_N),](/2012-wikipedia_en_all_nopic_01_2012/I/a7a686ba0d78476bcb17b47ce02539fc.png)